The tree chain splits

Pass to renumber all nodes in the tree , Make any path in the tree become O(logn) Segment continuous interval .

let me put it another way , The function of tree chain dissection That is to say ： Given Any tree , Put in the tree All points According to certain rules Number , Makes it A chain （ A sequence ）. After the transformation , Any path in the tree Can be transformed into In this sequence logn A continuous interval .

thus , about The problem of paths in trees , Can be successfully transformed into Interval problem .

for example , If we want to get The sum of the weights of each node in a path in the tree , perhaps Add a number to a path as a whole , Wait for a series of questions , We can turn it into Interval problem Solve , After that, we can generally use Line segment tree Conduct Section Maintenance of problems , Of course, it can also be used Tree array Etc. can be used for Maintain the data structure of the interval （ The core idea ）

Next let's see how it Specific operation Of ：（ how Transform a tree into a sequence , as well as How to convert each path in the tree into no more than logn Segment continuous interval ）

First of all, let's Build a tree ：

STEP I The concept is introduced

Define first Several concepts ：

• （1）“ Heavy son ” and “ Light son ”

Let's divide all the sons into Two kinds of ：“ Heavy son ” and “ Light son ”, Be careful , about leaf node No, “ son ” The concept . For... In the tree Any node , Here we use The root node For example , Can put all its sons There are two kinds of , First ask Each of its sub trees Of Total number of nodes .

As far as the picture above is concerned , The root node The first subtree on the left has 3 Nodes , The first subtree on the right has 4 Nodes , obviously The maximum number of nodes Yes. On the right side This subtree , that The root of the right subtree That is to say Of its parent node “ Heavy son ”, The corresponding figure below is Red nodes .

Be careful , If There are multiple subtrees with the maximum number of nodes , that Select the root node of any subtree As “ Heavy son ” that will do .

In addition to the heavy son, the son is called “ Light son ”.

And so on , The following figure 4 individual “ Red nodes ” Are all of their parent nodes “ Heavy son ”. The rest is “ Light son ”.

• （2）“ Heavy edge ” and “ Light side ”

“ Heavy son ” Corresponding “ Heavy edge ”,“ Light son ” Corresponding “ Light side ”.

namely ,“ Heavy son ” and Its parent node The connected edge is “ Heavy edge ”,“ Light son ” and Its parent node The connected edge is “ Light side ”（ except “ Heavy edge ” outside All sides of are called “ Light side ”）.

Corresponding to the figure below , all Red edge That is to say “ Heavy edge ”

• （3）“ heavy chain ”

This concept is only applicable to “ Heavy edge ”.

“ heavy chain ”, namely great A path consisting of multiple edges , Corresponding to the figure below The path under the red box That is to say “ heavy chain ”.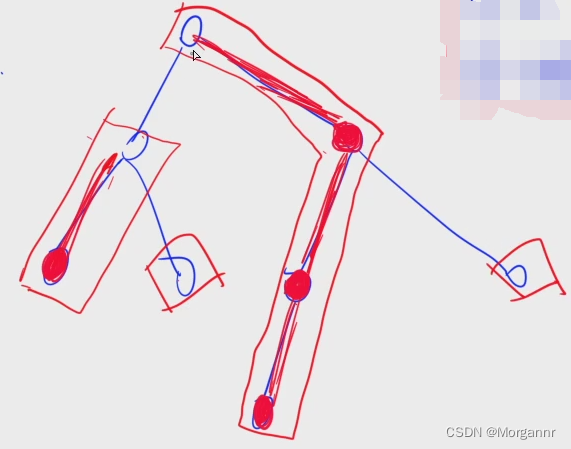

In the diagram above , We found two “ heavy chain ” All are Separate nodes , This is because ： We Put each node into one “ heavy chain ” in .

Here we can also find , The beginning of the heavy chain must be the light son .

STEP II Two times dfs Preprocessing （ The core ）

After introducing the concept , Let's draw a very important conclusion , This is also The tree chain splits Of emphasis ：

• Put in the tree All points and edges After classification , Any path in the tree can be split into O(logn) Continuous intervals .

that , How to turn the current tree into a sequence ？ We just use Of this tree dfs order , So-called dfs order , I've been in contact before , namely stay dfs In the process of , Traverse each point in order The order of the .

Take the root node as the 1 A little bit To traverse the , During traversal , We First traverse the current point “ Heavy son ”.

Pictured , The number marked above the node is dfs Traverse The order of time .

This traversal benefits ： Guarantee “ heavy chain ” All points on the are numbered consecutively .

thus , We'll take a tree according to its dfs order Turn into a chain .

To sum up ：（ Through the following two steps, you can turn the whole tree into a section dfs order , You can also mark each heavy chain ）

• First step , Through the first dfs In the tag tree Every point of the heavy son , That is to say dfs Record the size of each subtree in the process , After recursion of all sons , Determine which subtree has the most nodes , The root node of the subtree is the heavy son , Mark the .
  First pass dfs code snippet ：（ Pretreated at the same time depth Arrays are convenient for follow-up Mountain climbing Use ）

void dfs1(int u, int father, int dep)	// Node number   Its parent node number   Current depth 
{
    
	depth[u] = dep, fa[u] = father, sz[u] = 1;
	for (int i = h[u]; ~i; i = ne[i])
	{
    
		int j = e[i];
		if (j == father) continue;
		dfs1(j, u, dep + 1);
		sz[u] += sz[j];	// Current subtree size plus  j  The size of the tree  
		if (sz[son[u]] < sz[j]) son[u] = j;	// If the current number of nodes with multiple children is less than  j  The number of nodes of the tree , Explain that the current heavy son should be  j
	}
}

• The second step , After marking the heavy son , Do it again dfs, You can find out Each heavy chain 了 . stay The second time dfs meanwhile We can get dfs order , meanwhile Mark each heavy chain （ Just mark The vertex of each point on the heavy chain that will do , Like in the picture above , On a heavy chain 2、3、4 The vertices of node No. are 1 Number point ）
  Second times dfs code snippet ：（ Give priority to your son , Its benefits have been mentioned above ）

void dfs2(int u, int t)	// Current point   And the vertex of the heavy chain where the current point is located 
{
    
	id[u] = ++cnt; //dfs order 
	nw[cnt] = w[u];	//dfs Second in the preface cnt The weight of each point is w[u]
	top[u] = t;	// The vertex of the heavy chain where the current point is located is t
	if (!son[u]) return;	// If the current point is a leaf node , No son 
	dfs2(son[u], t);	// Otherwise, priority should be given to search for his son 
	// after dfs All light sons 
	for (int i = h[u]; ~i; i = ne[i])
	{
    
		int j = e[i];
		// If xx or j For his son , Because the heavy son has been searched , So skip the current loop 
		if (j == fa[u] || j == son[u]) continue;
		dfs2(j, j);	// Recursive light son , The top of the heavy chain where the light son is located is himself 
	}
}

STEP III Mountain climbing Split any path into intervals （ Inquire about or When modifying ）

After the first two steps , Now we want to Query a path or modify the value of a path when , We have to think about how Put in the tree Any path Split into O(logn) A continuous interval （ namely heavy chain ）？

This is actually one It's similar to asking for LCA The process of ：（ Mountain climbing ）

• There is... In the tree Two nodes a、b, There is a path between , Now split the path into Several heavy chains . Every time We are all separated find a、b The heavy chain of two points , Every time I find The vertex depth of the heavy chain is large （ a “ Short ”） The node of , And walk to its Parent node , Iteration goes up （b The other side of the node Also in the same way ）, Final , At two o 'clock I'm sure I'll come to The same heavy chain On （ namely At two o 'clock LCA The heavy chain ）, The middle part of two points Is the path The last paragraph .

code snippet ：（ Because the form of query path is the same as that of modification path , Let's take modification as an example ）

void modify_path(int u, int v, int k)	// Mountain climbing 
{
    
	// How to judge whether two points are in the same heavy chain ？
	// It's similar to parallel search   Save the vertex number of the heavy chain where each point is located 
	// Judge whether the vertices of the heavy chain where the two points are located are the same 
	while (top[u] != top[v])	// When two points are not in the same heavy chain 
	{
    
		if (depth[top[u]] < depth[top[v]]) swap(u, v);
		// Priority u Heavy chain 
		modify(1, id[top[u]], id[u], k);	// Modify this continuous interval   That is, subtree 
		u = fa[top[u]];	// Jump over the heavy chain 
	}
	if (depth[u] < depth[v]) swap(u, v);
	modify(1, id[v], id[u], k);	// Revise the last paragraph 
}

In this way , We will take a、b The path between two points is divided into several heavy chains , The number is O(logn) Level . Now we have successfully transformed the problem on the tree into logn An interval problem , After use Line segment tree perhaps Other data structures solve , Time complexity O(n * (logn ^ 2)). As shown in the figure below , The red part by heavy chain .

STEP IV Example

Let's look at a specific example ,

The question ：

Given a tree , Requirement realization Four operations ：

• Add a value to the weight of all points on the path between two nodes
• Add a value to the weight of all points in a certain tree
• Ask the sum of the weights of all points on the path between two points
• Ask the sum of the weights of all points in a certain tree

Ideas ：

basis The tree chain splits As a problem-solving idea , See the above thought explanation for details .

Time complexity ：

$O(n\ast (logn{)}^2)$

Code ：

#include <bits/stdc++.h>

using namespace std;
//#define map unordered_map
#define int long long
const int N = 1e5 + 10, M = N << 1;
int n, m;
int h[N], e[M], ne[M], w[N], idx;
int depth[N], fa[N], sz[N], son[N], top[N];
int id[N], nw[N], cnt;

struct node
{
    
	int l, r;
	int add, sum;
} t[N << 2];

inline void add(int a, int b)
{
    
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs1(int u, int father, int dep)
{
    
	depth[u] = dep, fa[u] = father, sz[u] = 1;
	for (int i = h[u]; ~i; i = ne[i])
	{
    
		int j = e[i];
		if (j == father) continue;
		dfs1(j, u, dep + 1);
		sz[u] += sz[j];
		if (sz[son[u]] < sz[j]) son[u] = j;
	}
}

void dfs2(int u, int t)
{
    
	id[u] = ++cnt, nw[cnt] = w[u], top[u] = t;
	if (!son[u]) return;
	dfs2(son[u], t);
	for (int i = h[u]; ~i; i = ne[i])
	{
    
		int j = e[i];
		if (j == fa[u] || j == son[u]) continue;
		dfs2(j, j);
	}
}

void pushup(int u) {
    
	t[u].sum = t[u << 1].sum + t[u << 1 | 1].sum;
}

void pushdown(int u) {
    
	auto& rt = t[u], & le = t[u << 1], & ri = t[u << 1 | 1];
	if (rt.add)
	{
    
		le.add += rt.add, le.sum += rt.add * (le.r - le.l + 1);
		ri.add += rt.add, ri.sum += rt.add * (ri.r - ri.l + 1);
		rt.add = 0;
	}
}

void build(int u, int l, int r)
{
    
	t[u] = {
     l, r };
	if (l == r) {
    
		t[u].sum = nw[r];//////////
		return;
	}
	int mid = l + r >> 1;
	build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
	pushup(u);
}

void modify(int u, int l, int r, int v)
{
    
	if (l <= t[u].l && r >= t[u].r)
	{
    
		t[u].add += v, t[u].sum += v * (t[u].r - t[u].l + 1);
		return;
	}
	pushdown(u);
	int mid = t[u].l + t[u].r >> 1;
	if (l <= mid) modify(u << 1, l, r, v);
	if (r > mid) modify(u << 1 | 1, l, r, v);
	pushup(u);
}

int ask(int u, int l, int r)
{
    
	if (l <= t[u].l && r >= t[u].r)
	{
    
		return t[u].sum;
	}
	pushdown(u);
	int mid = t[u].l + t[u].r >> 1;
	int res = 0;
	if (l <= mid) res += ask(u << 1, l, r);
	if (r > mid) res += ask(u << 1 | 1, l, r);
	return res;
}

void modify_path(int u, int v, int k)
{
    
	while (top[u] != top[v])
	{
    
		if (depth[top[u]] < depth[top[v]]) swap(u, v);
		modify(1, id[top[u]], id[u], k);
		u = fa[top[u]];
	}
	if (depth[u] < depth[v]) swap(u, v);
	modify(1, id[v], id[u], k);
}

int ask_path(int u, int v)
{
    
	int res = 0;
	while (top[u] != top[v])
	{
    
		if (depth[top[u]] < depth[top[v]]) swap(u, v);
		res += ask(1, id[top[u]], id[u]);
		u = fa[top[u]];
	}
	if (depth[u] < depth[v]) swap(u, v);
	res += ask(1, id[v], id[u]);
	return res;
}

void modify_tree(int u, int v)
{
    
	modify(1, id[u], id[u] + sz[u] - 1, v);
}

int ask_tree(int u)
{
    
	return ask(1, id[u], id[u] + sz[u] - 1);
}

signed main()
{
    
	cin >> n;
	for (int i = 1; i <= n; ++i) scanf("%lld", &w[i]);
	memset(h, -1, sizeof h);
	int t = n - 1;
	while (t--)
	{
    
		int x, y; scanf("%lld%lld", &x, &y);
		add(x, y), add(y, x);
	}
	dfs1(1, -1, 1);
	dfs2(1, -1);
	build(1, 1, n);
	cin >> m;
	while (m--)
	{
    
		int op, u;
		scanf("%lld%lld", &op, &u);
		if (op == 1)
		{
    
			int v, k; scanf("%lld%lld", &v, &k);
			modify_path(u, v, k);
		}
		else if (op == 2)
		{
    
			int k; scanf("%lld", &k);
			modify_tree(u, k);
		}
		else if (op == 3)
		{
    
			int v; scanf("%lld", &v);
			printf("%lld\n", ask_path(u, v));
		}
		else
		{
    
			printf("%lld\n", ask_tree(u));
		}
	}
	return 0;
}

（ Code + notes ）

#include <bits/stdc++.h>

using namespace std;
//#define map unordered_map
//#define int long long
const int N = 1e5 + 10, M = N << 1;
typedef long long ll;
int n, m;
int h[N], e[M], ne[M], w[N], idx;
int id[N];	// It turns out that every point in the tree is dfs Number in the sequence 
int nw[N];	// Weight of each numbered point , That is, the weight of the newly numbered point  dfs Second in the preface i A dot number 
int cnt;
int depth[N];	// The depth of each point 
int sz[N];	// The size of the subtree with each point as the root node 
int top[N];	// The vertex of the heavy chain where each point is located 
int fa[N];	// Each point parent node 
int son[N];	// Every point of the heavy son 

struct node
{
    
	int l, r;
	ll add, sum;	// Maintain two values in the segment tree  
} t[N << 2];

void add(int a, int b) {
    
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs1(int u, int father, int dep)	// Node number   Its parent node number   Current depth 
{
    
	depth[u] = dep, fa[u] = father, sz[u] = 1;
	for (int i = h[u]; ~i; i = ne[i])
	{
    
		int j = e[i];
		if (j == father) continue;
		dfs1(j, u, dep + 1);
		sz[u] += sz[j];	// Current subtree size plus  j  The size of the tree  
		if (sz[son[u]] < sz[j]) son[u] = j;	// If the current number of nodes with multiple children is less than  j  The number of nodes of the tree , Explain that the current heavy son should be  j
	}
}

void dfs2(int u, int t)	// Current point   And the vertex of the heavy chain where the current point is located 
{
    
	id[u] = ++cnt; //dfs order 
	nw[cnt] = w[u];	//dfs Second in the preface cnt The weight of each point is w[u]
	top[u] = t;	// The vertex of the heavy chain where the current point is located is t
	if (!son[u]) return;	// If the current point is a leaf node , No son 
	dfs2(son[u], t);	// Otherwise, priority should be given to search for his son 
	// after dfs All light sons 
	for (int i = h[u]; ~i; i = ne[i])
	{
    
		int j = e[i];
		// If xx or j For his son , Because the heavy son has been searched , So skip the current loop 
		if (j == fa[u] || j == son[u]) continue;
		dfs2(j, j);	// Recursive light son , The top of the heavy chain where the light son is located is himself 
	}
}

void pushup(int u)
{
    
	t[u].sum = t[u << 1].sum + t[u << 1 | 1].sum;
}

void pushdown(int u)	// Pass down the lazy sign 
{
    
	auto &rt = t[u], &le = t[u << 1], &ri = t[u << 1 | 1];
	if (rt.add)
	{
    
		le.add += rt.add, le.sum += rt.add * (le.r - le.l + 1);
		ri.add += rt.add, ri.sum += rt.add * (ri.r - ri.l + 1);
		rt.add = 0;
	}
}

void build(int u, int l, int r)
{
    
	t[u] = {
     l, r };
	if (l == r) {
    
		t[u].sum = nw[l];
		return;
	}
	int mid = l + r >> 1;
	build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
	pushup(u);
}

void modify(int u, int l, int r, int v)
{
    
	if (l <= t[u].l && r >= t[u].r)
	{
    
		t[u].add += v, t[u].sum += v * (t[u].r - t[u].l + 1);
		return;
	}
	pushdown(u);
	int mid = t[u].l + t[u].r >> 1;
	if (l <= mid) modify(u << 1, l, r, v);
	if (r > mid) modify(u << 1 | 1, l, r, v);
	pushup(u);
}

ll ask(int u, int l, int r)
{
    
	if (l <= t[u].l && r >= t[u].r)
	{
    
		return t[u].sum;
	}
	pushdown(u);
	int mid = t[u].l + t[u].r >> 1;
	ll res = 0;
	if (l <= mid) res += ask(u << 1, l, r);
	if (r > mid) res += ask(u << 1 | 1, l, r);
	return res;
}

void modify_path(int u, int v, int k)	// The mountain climbing method mentioned before 
{
    
	// How to judge whether two points are in the same heavy chain ？
	// It's similar to parallel search   I saved the vertex number of the heavy chain where each point is located 
	// Judge whether the vertices of the heavy chain where the two points are located are the same 
	while (top[u] != top[v])	// When two points are not in the same heavy chain 
	{
    
		if (depth[top[u]] < depth[top[v]]) swap(u, v);
		// Priority u Heavy chain 
		modify(1, id[top[u]], id[u], k);	// Modify this continuous interval   That is, subtree 
		u = fa[top[u]];	// Jump over the heavy chain 
	}
	if (depth[u] < depth[v]) swap(u, v);
	modify(1, id[v], id[u], k);	// Revise the last paragraph 
}

ll ask_path(int u, int v)	// The same as the modification form 
{
    
	ll res = 0;
	while (top[u] != top[v])
	{
    
		if (depth[top[u]] < depth[top[v]]) swap(u, v);
		res += ask(1, id[top[u]], id[u]);
		u = fa[top[u]];
	}
	if (depth[u] < depth[v]) swap(u, v);
	res += ask(1, id[v], id[u]);
	return res;
}

void modify_tree(int u, int v)	// With u The subtree is a continuous interval , The left and right endpoints are as follows 
{
    
	modify(1, id[u], id[u] + sz[u] - 1, v);
}

ll ask_tree(int u)
{
    
	return ask(1, id[u], id[u] + sz[u] - 1);
}

signed main()
{
    
	cin >> n;
	for (int i = 1; i <= n; ++i)
	{
    
		scanf("%d", &w[i]);
	}
	memset(h, -1, sizeof h);
	int t = n - 1;
	while (t--)
	{
    
		int u, v; scanf("%d%d", &u, &v);
		add(u, v), add(v, u);
	}

	dfs1(1, -1, 1);	// First ask the heavy son of each point 
	dfs2(1, -1);	// Please  dfs  order 
	build(1, 1, n);	// Build a line segment tree 

	// The tree chain splits 
	cin >> m;
	while (m--)
	{
    
		int t, u, v, k; scanf("%d%d", &t, &u);
		if (t == 1)
		{
    
			scanf("%d%d", &v, &k);
			modify_path(u, v, k);
		}
		else if (t == 2)
		{
    
			scanf("%d", &k);
			modify_tree(u, k);
		}
		else if (t == 3)
		{
    
			scanf("%d", &v);
			printf("%lld\n", ask_path(u, v));
		}
		else
		{
    
			printf("%lld\n", ask_tree(u));
		}
	}

	return 0;
}