当前位置:网站首页>Finishing of key concepts on deep neural networks exercises in the fourth week of in-depth learning
Finishing of key concepts on deep neural networks exercises in the fourth week of in-depth learning
2022-07-19 08:35:00 【l8947943】
Key Concepts on Deep Neural Networks
- What is the “cache” used for in our implementation of forward propagation and backward propagation?
- We use it to pass Z Z Z computed during forward propagation to the corresponding backward propagation step. It contains useful values for backward propagation to compute derivatives.
- It is used to cache the intermediate values of the cost function during training.
- It is used to keep track of the hyperparameters that we are searching over, to speed up computation.
- We use it to pass variables computed during backward propagation to the corresponding forward propagation step. It contains useful values for forward propagation to compute activations.
- Which of the following are “parameters” of a neural network? (Check all that apply.)
- L L L the number of layers of the neural network.
- W [ l ] W^{[l]} W[l] the weight matrices.
- g [ l ] g^{[l]} g[l] the activation functions.
- b [ l ] b^{[l]} b[l] the bias vector.
( Be careful ,W and b Is the parameter ,L and g Is a super parameter , The two are different concepts )
- Which of the following is more likely related to the early layers of a deep neural network?( Only provide correct answers )

- Vectorization allows you to compute forward propagation in an L-layer neural network without an explicit for-loop (or any other explicit iterative loop) over the layers l=1, 2, …,L. True/False?
- False
- True
- Assume we store the values for n [ l ] n^{[l]} n[l] in an array called layer_dims, as follows: layer_dims = [ n x n_x nx, 4,3,2,1]. So layer 1 has four hidden units, layer 2 has 3 hidden units and so on. Which of the following for-loops will allow you to initialize the parameters for the model?( Only provide correct answers )
- for i in range(1, len(layer_dims)):
parameter[‘W’ + str(i)] = np.random.randn(layer_dims[i], layer_dims[i-1]) * 0.01
parameter[‘b’ + str(i)] = np.random.randn(layer_dims[i], 1) * 0.01
- Consider the following neural network:

What are all the values of n [ 0 ] n^{[0]} n[0], n [ 1 ] n^{[1]} n[1], n [ 2 ] n^{[2]} n[2], n [ 3 ] n^{[3]} n[3] and n [ 4 ] n^{[4]} n[4]?
- 4, 4, 3, 2, 1
- 4, 3, 2, 1
- 4, 4, 3, 2
- 4, 3, 2
- During forward propagation, in the forward function for a layer l l l you need to know what is the activation function in a layer (sigmoid, tanh, ReLU, etc.). During backpropagation, the corresponding backward function also needs to know what is the activation function for layer l l l, since the gradient depends on it. True/False?
- False
- True
- For any mathematical function you can compute with an L-layered deep neural network with N hidden units there is a shallow neural network that requires only log N \log N logN units, but it is very difficult to train.
- False
- True
( reason :On the contrary, some mathematical functions can be computed using an L-layered neural network and a given number of hidden units; but using a shallow neural network the number of necessary hidden units grows exponentially.)
- Consider the following 2 hidden layers neural network:

Which of the following statements are true? (Check all that apply).
- W [ 2 ] W^{[2]} W[2] will have shape (3, 1)
- W [ 2 ] W^{[2]} W[2] will have shape (4, 3)
- W [ 1 ] W^{[1]} W[1] will have shape (3, 4)
- W [ 2 ] W^{[2]} W[2] will have shape (3, 4)
- b [ 1 ] b^{[1]} b[1] will have shape (1, 3)
- W [ 1 ] W^{[1]} W[1] will have shape (4, 3)
- b [ 1 ] b^{[1]} b[1] will have shape (4, 1)
- b [ 1 ] b^{[1]} b[1] will have shape (3, 1)
- W [ 2 ] W^{[2]} W[2] will have shape (1, 3)
- Whereas the previous question used a specific network, in the general case what is the dimension of b [ l ] b^{[l]} b[l], the bias vector associated with layer l?
- b [ l ] b^{[l]} b[l] has shape (1, n [ l − 1 ] n^{[l−1]} n[l−1])
- b [ l ] b^{[l]} b[l] has shape ( n [ l − 1 ] n^{[l−1]} n[l−1],1)
- b [ l ] b^{[l]} b[l] has shape ( n [ l ] n^{[l]} n[l],1)
- b [ l ] b^{[l]} b[l] has shape (1, n [ l ] n^{[l]} n[l])
边栏推荐
- New data type of redis bitmaps
- 5.1 security vulnerabilities and Prevention
- 49、Mysql使用
- Consul service registration and discovery
- 6-9 vulnerability exploitation telnet login rights lifting
- JS学习笔记14-15:JS数组及数组字母量
- Redis介绍
- Obtain the home location through IP
- 力扣382链表随机节点笔记
- Super dry! Thoroughly understand golang memory management and garbage collection
猜你喜欢

46、IO模型

Excellent résumé! Enfin quelqu'un a compris toutes les connexions SQL

New data type of redis bitmaps

Super dry! Thoroughly understand golang memory management and garbage collection
![leetcode:287. Find the repetition number [fast and slow pointer board]](/img/4c/6278584f528f00776ed75f846edb3a.png)
leetcode:287. Find the repetition number [fast and slow pointer board]

Enjoy JVM -- knowledge about GC garbage collection

3D激光SLAM:ALOAM---帧间里程计代码解读

matlab导入小数点后9位以上的浮点数

Hand in hand practice a DAPP, the road to Web3.0!
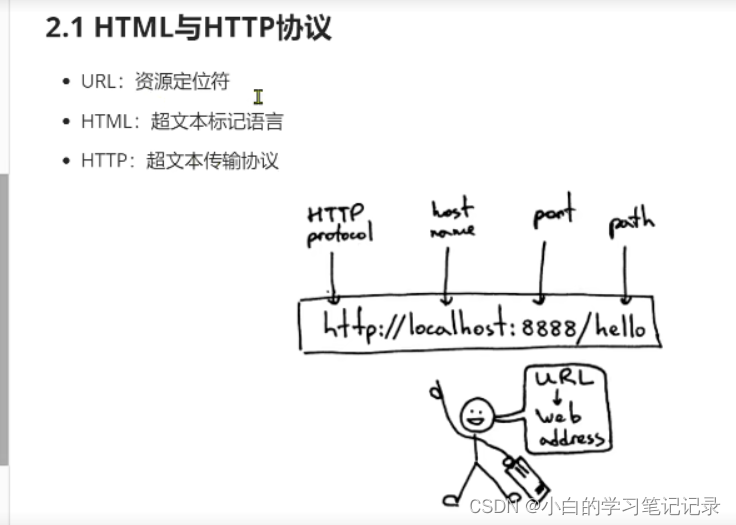
Dark horse programmer - software testing -16 stage 3 - function testing -175-198, URL composition introduction, request content and composition description line function test and database, URL composi
随机推荐
Redis的发布和订阅
The latest generation of Internet: Web 3.0
60. Initial knowledge of wsgiref handwritten web framework +jinja2 module
力扣455分发饼干笔记
Super dry! Thoroughly understand golang memory management and garbage collection
1、flask基础
JS学习笔记06-08:数组的遍历以及数组的四个方法
5.2 数据库安全
全志V3s学习记录(13)OV2640的使用
百度Apoll
#yyds干货盘点#Cross-origin 跨域请求
SPARK闲杂--为什么复用Exchange和subquery
创建静态库的基本步骤
3D laser slam:aloam --- interpretation of inter frame odometer code
Redis常用数据类型——Redis列表(List)和Redis 集合(Set)
Can seaport and erc-4907 become new ways to release NFT liquidity| Tokenview
OpenFeign服务接口调用
使用toruch.nn搭建最简单的神经网络骨架
力扣1669合并两个链表笔记
力扣43字符串相乘笔记