当前位置:网站首页>(codeforce631) c.report (monotone stack)
(codeforce631) c.report (monotone stack)
2022-07-18 08:53:00 【AC__ dream】
Topic link :Problem - 631C - Codeforces

The sample input :
3 1
1 2 3
2 2
Sample output :
2 1 3 The question : Given a length of n Array of , Then give m operations
The format of the operation :
1 r, Sub sequence a[1]~a[r] Sort from small to large
2 r, Sub sequence a[1]~a[r] Sort from large to small
Let's output the sequence after the operation , Note that there are multiple sets of samples
analysis : Let's take a look at the characteristics of these operations :
If we are right now 7 Elements in ascending order , And then to the front 10 Elements in descending order , Then we still need to face the front 7 Are the elements in ascending order ? In fact, it is obviously unnecessary , because When the later operation range is larger than the current operation range , The current operation must be directly modified by the operation with a larger operation range , So this also gives us an inspiration , The scope of effective operation must be smaller and smaller , Effective operation means that there is no operation beyond the current operation , Obviously, this can be handled directly with monotone stack , Then our effective operation range is a monotonically decreasing sequence , But let's think about another problem , Suppose two effective operations are of the same nature , That is, when two adjacent operations are in ascending or descending order , Because the scope of the following operations is smaller , So the following operations have no substantive significance , We can also eliminate this kind of operation , Then the remaining effective operations are those that satisfy the following two properties :
1. The operating range gradually decreases
2. Two adjacent operations must be in ascending and descending order
With these operations, let's analyze how to operate to get the final sequence
First The part that is not operated in the maximum operation range is the number corresponding to the original sequence , We sort the remaining numbers from small to large , If the current operation is an ascending operation , Explain that the previous operation is a descending operation , Then suppose the scope of the current operation is r1, The scope of the last operation is r2, So there are r2>r1, After the last operation, it is a descending sequence , Then the number of ranges that cannot be covered by the current operation has been fixed , It can't be updated by subsequent operations , So we can select some numbers from the sequence sorted from small to large and fill them in the area that the corresponding current operation cannot cover , Similarly, if the current operation is a descending operation and the previous operation is an ascending operation , We can select some numbers from the sequence sorted from small to large, and fill them in the corresponding areas that cannot be covered by the current operation , We can operate this process with double pointers , So the complexity of the whole subject is O(n) 了 , There may be a lot of details , You can take a good look at the code .
Here is the code :
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
using namespace std;
const int N=2e5+10;
int r[N],op[N],a[N],ans[N];
int st[N],tt;
int main()
{
int n,m;
while(scanf("%d%d",&n,&m)!=EOF)
{
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=m;i++)
scanf("%d%d",&op[i],&r[i]);
tt=0;
for(int i=1;i<=m;i++)
{
while(tt&&r[st[tt]]<=r[i]) tt--;// Deal with effective operations with monotonic stack
if(!tt) st[++tt]=i;
else if(op[st[tt]]!=op[i]) st[++tt]=i;// When the two do the same sort, there is no need to do
}
for(int i=r[st[1]]+1;i<=n;i++)
ans[i]=a[i];
sort(a+1,a+r[st[1]]+1);
int ll=1,rr=r[st[1]];
r[st[tt+1]]=0;
if(op[st[tt]]==1) op[st[++tt]]=2;
else op[st[++tt]]=1;
for(int i=2;i<=tt;i++)
{
if(op[st[i]]==1)// Currently in ascending order
for(int j=r[st[i-1]];j>r[st[i]];j--)
ans[j]=a[ll++];// Take some numbers from small to large
else
for(int j=r[st[i-1]];j>r[st[i]];j--)
ans[j]=a[rr--];
}
for(int i=1;i<=n;i++)
printf("%d ",ans[i]);
puts("");
}
return 0;
}边栏推荐
- Harmonic cloud classroom | agile development process and project practice sharing
- Measurement of conductive potential of thin film copper foil
- VBA drives SAP GUI to complete initialization of interface element value
- 洞悉数据库迷局,2022金仓创新产品发布会召开
- 关于2022年3月APT-C-41伪装为WinRar.exe攻击的终端侧应急响应排查点
- Event 4624 is login successful!?! Is that true?
- HybridCLR——划时代的Unity原生C#热更新技术
- (2021 Niuke multi school III) j-counting triangles (thinking)
- Leetcode exercise - Sword finger offer 32 - ii Print binary tree II from top to bottom
- HMS core graphics and image technology shows the latest functions and application scenarios, and accelerates the construction of digital intelligence life
猜你喜欢
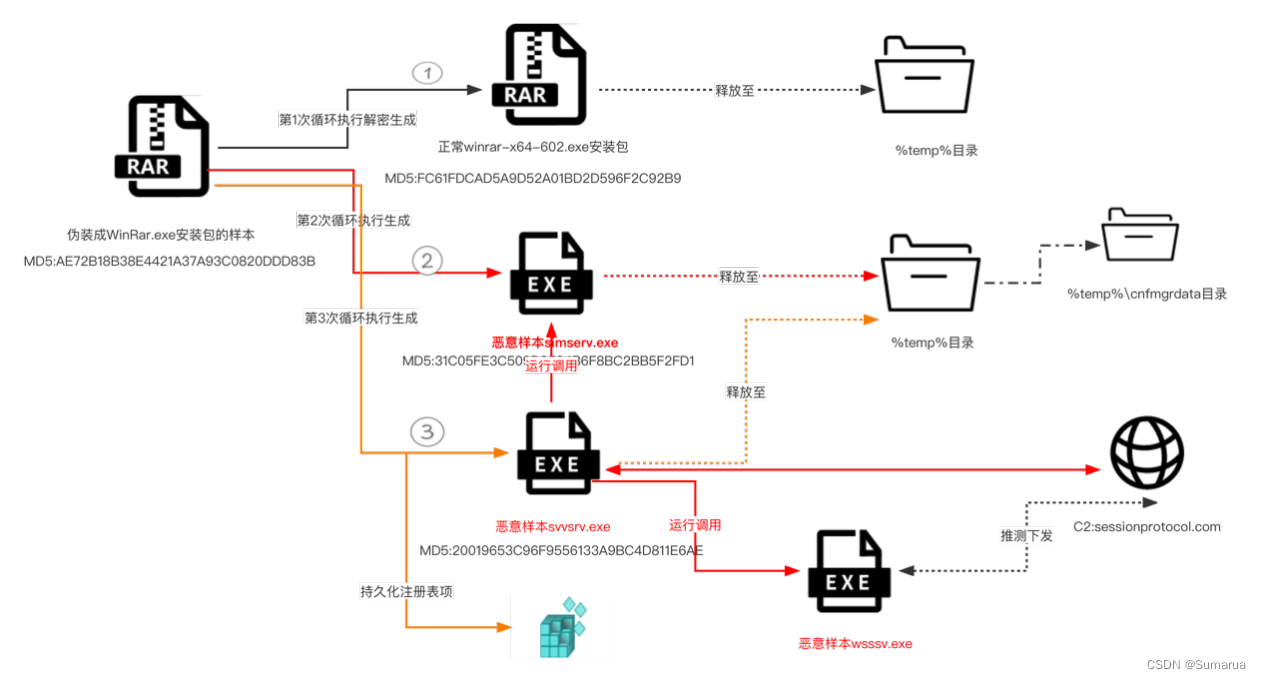
About March 2022, apt-c-41 disguised as winrar Exe attack terminal side emergency response troubleshooting point

健康防猝指南1:体重和减肥的秘密

金融、生物医药、集成电路,上海巨头行业用AI加持核心竞争力

Event 4624 is login successful!?! Is that true?

(2021牛客多校五)D-Double Strings(乘法原理+动态规划)

【无标题】

(2021 Niuke multi school III) j-counting triangles (thinking)

使电脑拥有公网IP方法
档案的逻辑 | 全宗区分和示例

How to clean up your email subscriber list to improve email marketing
随机推荐
【集训DAY2】Torch bearer【暴力】【DFS】
[leetcode string -- public prefix] bm84 Longest Common Prefix
PCIE知识点-011:PCIE 配置能力结构与协议版本的关系
国内外知名的待办事项app
(codeforce631)C.Report(单调栈)
达芬奇pro的FPGA学习笔记6.2--vcs和verdi开发蜂鸟e203
DNS攻击防护原理
Leetcode 151. 颠倒字符串中的单词
[untitled]
Honghu Wanlian Zhiyuan development board is officially integrated into the openharmony backbone
Modifying background photos and using skills of idea
Basic learning about MySQL
The solution of starting the server is stuck during MySQL installation
开发命令行工具
In the throes of household appliance market transformation, SaaS system platform is applied to inject new momentum into the development of household appliance industry
HMS Core图形图像技术展现最新功能和应用场景,加速构建数智生活
在线SQL转YAML工具
Flink 资源管理详解
DNS attack protection principle
使电脑拥有公网IP方法