当前位置：网站首页>Detailed explanation of Euler angle, axis angle, quaternion and rotation matrix

Detailed explanation of Euler angle, axis angle, quaternion and rotation matrix

2022-07-19 11:00:00 【TT ya】

Beginner little rookie , I hope it's like taking notes and recording what I've learned , Also hope to help the same entry-level people , I hope the big guys can help correct it ~ Tort made delete .

Catalog

One 、 Euler Angle

1、 Static definition

2、 Representation of Euler angle

3、 Advantages and disadvantages of Euler angle

4、 The universal joint of Euler angle is deadlocked （ There is no problem of universal lock in static state ）

Two 、 Four yuan number

1、 Propose meaning and definition （ Including shaft angle ）

3、 Polar form of quaternion

4、 Examples of the use of quaternions

5、 Advantages and disadvantages of quaternion

3、 ... and 、 The mutual transformation between quaternions and Euler angles

1、 Quaternion to Euler angle

2、 Euler angle to Quaternion

Four 、 Rotation matrix

One 、 Euler Angle

1、 Static definition

For a reference system in three-dimensional space , The orientation of any coordinate system , Can be represented by three Euler angles .

The reference system is also called laboratory reference system , It's stationary .
The coordinate system is fixed to the rigid body , Rotate with the rotation of the rigid body .

Let's take a classic example ：

Set up xyz- The axis is the reference axis of the reference system （ That is, the blue part in the figure below ）. call xy- Plane and XY- The intersection of planes is the intersection line , In English letters （N） representative .zxz The Euler angle of compliance can be statically defined in this way ：

α yes x- The angle between the axis and the intersection line ,
β yes z- Shaft with Z- Angle between axes ,
γ Is the intersection line and X- Angle between axes .

But for the order and marking of included angles , Designation of two axes of included angle , There are no regular rules . So whenever Euler angle is used , We must clearly show the order of included angles , Specify its reference axis

2、 Representation of Euler angle

First round z Shaft rotation α horn （ If left ）, Then around X’ Shaft rotation β horn （ As shown in the middle ）, The last is around Z’ Shaft rotation γ horn （ Like the picture on the right ）, This is a zxz Compliance （ Go around first z Axis , Rewind x Shaft rewinding z‘ Axis ） Euler angle representation of .（ except zxz There are other specified methods besides compliance , Such as xyx,zyz. I won't go into details here ）

Euler angles include 3 Turns , According to this 3 Rotate to specify the orientation of a rigid body . this 3 Rotate around x Axis ,y Axis and z Axis , Known as Pitch,Yaw and Roll.

3、 Advantages and disadvantages of Euler angle

advantage ：

（1） Euler angle consists of three angles , intuitive , Easy to understand .
（2） It can rotate from one direction to another for more than 180 Degree angle .

shortcoming ：

（1） Euler angle is not transitive , The order of rotation affects the result of rotation , Different applications may use different rotation sequences , The rotation order cannot be unified ;
（2）3 The rotation angle can be unlimited , That is to say, the value range is （-inf,inf）;
（3） It may cause the universal joint to deadlock

4、 The universal joint of Euler angle is deadlocked （ There is no problem of universal lock in static state ）

For dynamic Euler angle （ Rotate around the object coordinate system ）, No matter around the first , What is the rotation angle of the three axes , As long as the rotation angle around the second axis is ±90°, There will be universal lock phenomenon .

Universal lock phenomenon ： Once you choose ±90° As pitch horn , This will cause the first rotation to be equivalent to the third rotation , The entire rotation means that the system is limited to rotation around the vertical axis , Missing a representation dimension .

For example ：
For example, let's go around z The shaft rotates at any angle , Get the figure below, right
Then let's go around y pivot 90 degree , Get the picture below （ here Z’ The axis is in blue x-y In the plane ）
Then no matter how we go around X‘ Shaft rotation ,Z’ The axis is always blue x-y In the plane , It's like being locked .

Avoidance of universal lock ： Limit the angle range of rotation —— The rotation angle around the first axis is limited to ±180° between ; The limit around the second axis is ±90° between .

Two 、 Four yuan number

1、 Propose meaning and definition （ Including shaft angle ）

Put forward the meaning ： The above Euler angle can only be obtained after multiple rotations , Then why not do it in one step , Only rotate once ？ Then quaternion came into being .

Definition ：

For the rotation of an object , We only need to know four values ： A rotating vector + An angle of rotation . And quaternion is exactly such a design ：

q = (x,y,z,w)

among x,y,z Represents the three-dimensional coordinates of the vector ,w It represents the angle

Actually , Quaternion is essentially a hypercomplex :

$q=x i+y j+z k+w, i^{2}=j^{2}=k^{2}=-1 ,i*j = k\\$

Axis angle

$\quad q=\left[\begin{array}{ll} \vec{v} & w \end{array}\right]=([x,y,z]^{T},\theta)$ —— This is an axis vector （ Unit vector ） The expression of adding a rotation angle is the axis angle expression .

The biggest limitation of shaft angle is that simple interpolation cannot be carried out ;
Besides , Rotation in the form of shaft angle cannot be directly applied to points or vectors , Must be converted to matrix or quaternion .

2、 Related calculation rules of quaternions

（1） Add

$q1+q2 = [\overrightarrow{v1}+\overrightarrow{v2},w1+w2]$

（2） Multiplication

$p_{1} p_{2}=\left(\overrightarrow{v_{1}} \times \overrightarrow{v_{2}}+\omega_{1} * \overrightarrow{v_{2}}+\omega_{2} * \overrightarrow{v_{1}}, \quad \omega_{1} \omega_{2}-\overrightarrow{v_{1}} \cdot \overrightarrow{v_{2}}\right)$

The unit is 4 yuan —— For convenience , Regular regulations ：

$x^{2}+y^{2}+z^{2}+w^{2}=1$

At this time, the complex multiplication can be expressed as ：

It can also be expressed in matrix form

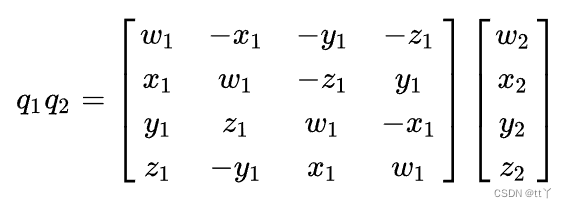
（3） conjugate —— $(-\overrightarrow{v1},w1)$

3、 Polar form of quaternion

$q=\|q\|[\vec{n} \cdot \sin \theta, \cos \theta]$

among ||q|| Represents the modulus of quaternion , The unit quaternion modulus is 1, and θ Is the half width of the rotation process represented by quaternions , in other words 2θ Is the size of the rotation angle ,n Is the unit vector representing the direction of the rotation axis .

4、 Examples of the use of quaternions

A vector ：v1, Let it go around v2 rotate θ degree （ Turn it clockwise ）

So there are p = (v1, 0); q = ( v2 * sin(θ/2) , cos(θ/2) )

The quaternion after rotation is （ The real part of the quaternion obtained is 0, The imaginary part is the new coordinate ）： $p^{\prime}=q p q^{-1}$

5、 Advantages and disadvantages of quaternion

advantage ：

Small storage space , High calculation efficiency .
There is no universal joint lock problem in quaternion rotation .

shortcoming ：

The numerical representation of quaternions is not intuitive .
A single quaternion cannot represent more than... In any direction 180 The rotation of the degree of .

3、 ... and 、 The mutual transformation between quaternions and Euler angles

1、 Quaternion to Euler angle

Set up —— $|q|^{2}=w^{2}+x^{2}+y^{2}+z^{2}=1$

${\left[\begin{array}{c} \text { roll } \\ \text { pith } \\ y a w \end{array}\right]=\left[\begin{array}{c} \phi \\ \theta \\ \psi \end{array}\right]=\left[\begin{array}{l} \operatorname{atan} 2\left(\frac{2(z y+w x)}{w^{2}-x^{2}-y^{2}+z^{2}}\right) \\ \arcsin (a(w y-x z)) \\ \operatorname{atan2}\left(\frac{2(x y+w z)}{w^{2}+x^{2}-y^{2}-z^{2}}\right) \end{array}\right]=\left[\begin{array}{c} \operatorname{atan} 2\left(\frac{2(z y+w x)}{1-2\left(x^{2}+y^{2}\right)}\right) \\ \arcsin (a(w y-x z)) \\ \operatorname{atan2}\left(\frac{2(x y+w z)}{1-2\left(y^{2}+z^{2}\right)}\right) \end{array}\right]}$

2、 Euler angle to Quaternion

We set up

Then there are ：

$q=\left[\begin{array}{l} w \\ x \\ y \\ z \end{array}\right]=\left[\begin{array}{l} \cos (\phi / 2) \cos (\theta / 2) \cos (\psi / 2)+\sin (\phi / 2) \sin (\theta / 2) \sin (\psi / 2) \\ \sin (\phi / 2) \cos (\theta / 2) \cos (\psi / 2)-\cos (\phi / 2) \sin (\theta / 2) \sin (\psi / 2) \\ \cos (\phi / 2) \sin (\theta / 2) \cos (\psi / 2)+\sin (\phi / 2) \cos (\theta / 2) \sin (\psi / 2) \\ \cos (\phi / 2) \cos (\theta / 2) \sin (\psi / 2)-\sin (\phi / 2) \sin (\theta / 2) \cos (\psi / 2) \end{array}\right]$

Four 、 Rotation matrix

Hypothetical winding XYZ The rotation angles of the three axes are α ,β ,γ , Then the calculation method of rotation matrix of cubic rotation is as follows ：

$\begin{array}{l} R_{x}(\alpha)=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha \\ 0 & \sin \alpha & \cos \alpha \end{array}\right] \\ R_{y}(\beta)=\left[\begin{array}{ccc} \cos \beta & 0 & \sin \beta \\ 0 & 1 & 0 \\ -\sin \beta & 0 & \cos \beta \end{array}\right] \\ R_{z}(\gamma)=\left[\begin{array}{ccc} \cos \gamma & -\sin \gamma & 0 \\ \sin \gamma & \cos \gamma & \\ 0 & 0 & 1 \end{array}\right] \end{array}$

If pressed Z-Y-X Rotation order （ It means first around its own axis Z, Then around its own axis Y, Finally, around its own axis X）, Then the rotation matrix is ：

$R=R_{z}(\gamma) * R_{y}(\beta) * R_{x}(\alpha)$