Important algorithms

• Sort: Insertion sort, merge sort, quick sort
• Binary search
• Graph: BFS、DFS and their application
• Greedy: Dijkstra’s algorithm and improved implementation
• Dynamic programming: Bellman-Ford
• Network flow: Ford-Fulkerson algorithm
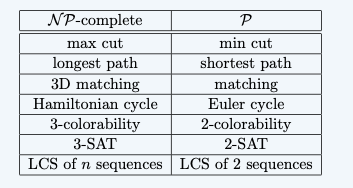
• NPC: Vertex Cover(D), Independent Set(D), SAT, 3SAT, integer programming
• Linear programming (integer programming)

Note

重点是理解各种算法的应用以及时间复杂度。

Lecture1: Insertion sort, efficient algorithm

Insertion sort

Analysis of algorithms

• Correctness: Proof by induction.
• Running time: Best case: 5n − 4; worst case. 3n^2 + 7n − 4
• Space: in-place algorithm

Efficient algorithms (polynomial running time)

Lecture2: Merge sort

Asymptotic notation

• Asymptotic upper bounds: Big-O notation
• Asymptotic lower bounds: Big-Ω notation
• Asymptotic tight bounds: Θ notation
• Asymptotic upper bounds that are not tight: little-o
• Asymptotic lower bounds that are not tight: little-ω

Divide & conquer principle, application: merge sort

• Correctness
• Running time: O(nlogn)
• Space: Θ(n)

Solving recurrences and running time of merge sort

• recursion trees
• Master theorem

Lecture3: Binary search, quicksort

Binary search

• Running time: O(log n)

Quicksort

• divide and conquer
• Space: in-place
• Running time:
• Its worst-case running time is Θ(n^2) but its average-case running time is Θ(nlogn)
• Correctness:
  • strong induction (the induction step at n requires that the inductive hypothesis holds at all steps 1, 2, …, n−1 and not just at step n−1, as with simple induction.)

Lecture5: Graphs, Breadth-First Search (BFS)

Definition

• Undirected / directed
• Simple: all vertices are distinct.

• An undirected graph is connected when there is a path between every pair of vertices.
• The connected component of a node u is the set of all node in the graph reachable by a path from u.
• A directed graph is strongly connected if for every pair of vertices u, v, there is a path from u to v and from v to u.
• The strongly connected component of a node u in a directed graph is the set of nodes v in the graph such that there is a path from u to v and from v to u.

• Tree: connected acyclic graph
• Bipartite graphs
• Degree theorem
• Linear graph algorithms run in O(n+m) time

Representing graphs

• adjacency matrix
• adjacency list

Breadth-first search (BFS)

• queue: FIFO data structure
• s-t connectivity
• shortest s-v paths in unweighted graphs.
• Connected components in undirected graphs
• Testing bipartiteness & graph 2-colorability
• SCC(u): SCC of node u
• All SCC: but not linear

Lecture6: Depth-first search, topological sorting

Depth-first search (DFS)

• stack: LIFO (Last-In First-Out)
• s-t connectivity
• Cycle detection
• Topological sorting in DAGs (directed acyclic graph)
  • Run DFS(G); compute finish times.
  • Process the tasks in decreasing order of finish times.
  • Running time: O(m+n)
  • different edges: forward, back, cross --> time intervals for vertices
• Undirected graphs: find all connected components
• SCC(u): SCC of node u
• All SCC: linear
  • Compute Gr.
  • Run DFS(Gr); compute finish(u) for all u.
  • Run DFS(G) in decreasing order of finish(u).
  • Output the vertices of each tree in the DFS forest of line 3 as an SCC.

Lecture7&8: Strongly connected components, single-origin shortest paths in weighted graphs

Applications of DFS: Strongly connected components

(combine it with the above)

Shortest paths in graphs with non-negative edge weights (Dijkstra’s algorithm)

• Greedy principle
• implementation and improved implementation
• running time

Lecture12: Data compression and Huffman coding

• Prefix codes and trees
• The Huffman algorithm

Lecture9: The dynamic programming principle; segmented least squares

• Overlapping subproblems
• An easy-to-compute recurrence
• Iterative, bottom-up computations

• Segmented least squares
• Sequence alignment

After midterm

Lecture 11 Shortest paths in weighted graphs (Bellman-Ford)

• Bellman-Ford algorithm (DP solution)
  • OPT (i, v) = cost of shortest s-v path using at most I edges
  • 二维数组: time: O(nm), space: O(n^2)
    • Pseudocode: M [i, v]
  • 一维数组: time: O(nm), space: O(n)
    • Early termination condition: if at some iteration I no value in M changed, then stop.
    • Pseudocode: M[v] similar to Dijkstra algorithm
  • Detecting negative cycle
    • Update all edges n times (1 more time)

Lecture 15&16 Network flows

Definition:

• Capacity constrains
• Flow conservation
• |f| = f_out
• Max flow and min cut

Residual graph and augmenting paths

• Residual graph (forward, backward)
• P is simple path. Augment f by pushing extra flow on P
• Bottleneck

Ford-Fulkerson algorithm

• Running time: O(nmU) —— pseudo-polynomial
• Correctness
• Application: max bipartite matching
• Reduction (Forward direction, Reverse direction)

Lecture 20&21 Reductions; independent set and vertex cover; decision problems

Reduction:

• x of X
• y=R(x) of Y

Reduction as a means to design efficient algorithm

• Y has polynomial computational steps
• Call polynomial number of Y
• X <= pY

Reduction as a means to argue about hard problems

• X <= p Y
• Y is at least as hard as X
• If X cannot be solved in polynomial time, then Y cannot.
• Relative level of difficulty: X <= pY, Y <= pX

Two hard problems

• Independent set
• Vertex cover

Optimization versions for IS and VC

• Max independent size
• Min vertex cover

Decision version of optimization problems

• Yes/no answer
• Max – lower, min – upper

Rough equivalence of decision & optimization problems

• Suppose we have an algorithm to solve MIS we can use it to solve IS(D)
• Suppose we have an algorithm to solve IS(D) we can use it to solve MIS

Reduction from Independent Set to Vertex Cover

• Forward direction
• Reverse direction

Class P

• Set of decision problems that can be solved by polynomial-time algorithm.

（引出NP）

• If we were given a solution S for such a problem X(D), we could check if it is correct quickly.
• Such an S is a succinct certificate that x 属于X(D)

Class NP

• An efficient certifier (or verification algorithm) B for a problem X(D) is a polynomial algorithm that

  • Takes two input arguments: instance x (which is a specific input of the problem) and the short certificate t
  • B(x, t) = yes and |t| <= Poly(|x|), then we have x 属于 X(D)

• Set of decision problems that have an efficient certifier.

P vs NP

• P 属于 NP
• P = NP ?
• Why would NP contain more problems than P? Intuitively, the hardest problems in NP are the least likely to belong to P

NPC

• The hardest problems
• NPC X(D) 定义：
  • If X(D) 属于 NP
  • For all Y 属于 NP, Y <= p X(D)

Show a problem is NP-complete

• Suppose we had an NP-complete problem X, to show Y is NPC, we only need to show:
  • Y 属于 NP
  • X <= p Y
• (相比根据定义证明NPC，这种方法只需要做一次reduction，简化了很多）

Lecture 22 Satisfiability problems: SAT, 3SAT, Circuit-SAT

Definition

• truth assignment
• A truth assignment satisfies a clause if it causes the clause to evaluate to 1.
• A formula φ is satisfiable if it has a satisfying truth assignment.

Satisfiability (SAT) and 3SAT

• SAT: Given a formula φ in CNF with n variables and m clauses, is φ
  satisfiable?
• 3SAT: Given a formula φ in CNF with n variables and m clauses such that each clause has exactly 3 literals, is φ satisfiable?

The art of proving NP-completeness

• Circuit-SAT ≤p SAT
• SAT ≤P 3SAT
• 3SAT ≤p IS(D)

Lecture 23&25 Representative NP-complete problems: TSP, Set Cover

• Circuit SAT
• TSP
• Integer programming
  

Lecture18&19 Linear programming

Definition

• feasible solutions
• Feasible region
• Optimal solution

Duality

• We can alternatively solve the dual to find the optimal objective value.

• An optimal dual solution can be used to derive an optimal primal solution (complementary slackness).

• The dual may have structure making it easier to solve at scale (e.g., via parallel optimization).

• 7-step dualization

formulating LPs

• 将其他形式的问题转化为LP或IP