Preface

Suppose there is n The super washing machine is on the same row . At the beginning , There may be a certain amount of clothes in each washing machine , Or it could be empty .

In each step , You can choose whatever m (1 <= m <= n) Washing machine , At the same time, send a piece of clothes from each washing machine to an adjacent washing machine .

Given an array of integers machines Represents the number of clothes in each washing machine from left to right , Please give the number of clothes left in all washing machines equal Minimum number of operation steps . If you can't make the number of clothes in each washing machine equal , Then return to -1 .

source ： Power button （LeetCode）
link ：https://leetcode.cn/problems/super-washing-machines
Copyright belongs to the network . For commercial reprint, please contact the official authority , Non-commercial reprint please indicate the source .

One 、 Their thinking

Ideological tradition : The bottleneck of single point , Finally, look at the relationship between the total answer and the single point bottleneck
Suppose you come to a certain station (i Number ) Washing machine Number of clothes ?

Suppose we know the average of each machine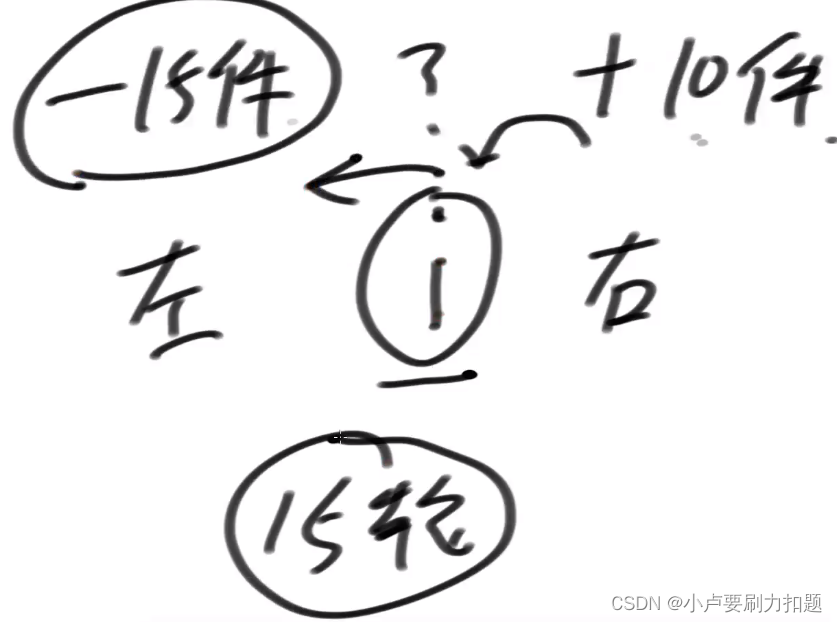

The left side is under 15 Pieces of . And there are many on the right side 10 Pieces of , Suppose there are always clothes to move , At least a few rounds .

At the very least 15 round

i If there are very few clothes, you may have to give it clothes on both sides

At least it needs 15 round

If the left side owes 15 Pieces of . On the right side 7 Pieces of , I ask how many rounds you want to move , Both sides are counting on i output , It can only throw one at a time .
Therefore need 22 round

First calculate the total number of clothes , You can calculate the cumulative sum of the left part , i The position has its own value .
There are still a few more pieces on the left side , Is the right part short or extra . Can be calculated
There is a total number of clothes , There is one i The cumulative sum on the left , Next you go to any one i Location .
Your left side , Is the right side more or less ? You can figure it out

According to our strategy . We figure out how many rounds the bottleneck takes at zero ,1 How many rounds does the bottleneck need in position ,
2 How many rounds does the bottleneck need in position , Each bit We should talk more about the bottleneck of setting . The conclusion is the most painful point of all the answers max, Determines the overall bottleneck .
Because when the most painful bottleneck is satisfied , The other bottleneck synchronization is solved
Because he can move in parallel in each round . So your most painful bottleneck determines the total number of rounds . No, why is mathematical proof troublesome

Code

class Solution {
    
    public int findMinMoves(int[] arr) {
    
        if (arr == null || arr.length == 0) {
    
			return 0;
		}
        int size=arr.length;
        int sum=0;
        for(int i=0;i<size;i++){
    
            sum+=arr[i];
        }
        if(sum%size!=0){
    
            return -1;
        }
        int avg=sum/size;
        int leftSum=0;
        int ans=0;
        for(int i=0;i<size;i++){
    
            //  The number of differences on the left 
            int leftRes=leftSum-i*avg;
            //  The number of differences on the right 
            int rightRes=(sum-leftSum-arr[i])-(size-i-1)*avg;
            if(leftRes<0&&rightRes<0){
    
                ans=Math.max(ans,Math.abs(leftRes)+Math.abs(rightRes));
            }else{
    
                ans=Math.max(ans,Math.max(Math.abs(leftRes),Math.abs(rightRes)));
            }
            leftSum+=arr[i];
        }
        return ans;
    }
}