[C data storage]

Catalog

One 、 Basic classification of data types

Two 、 The storage of integers

         The original code, the reverse code, the complement code

         Byte order at the large and small end

         Exercise one

         Exercise 2

3、 ... and 、 Floating point storage

One 、 Basic classification of data types

signed： A signed

unsigned： Unsigned

Data in memory defaults to signed, except char,char Whether there are symbols depends on different compilers .

integer ：

char（char The essence of type is ASCII Code value ）、short、int、long

floating-point ：

float、double

Construction type ：

         An array type ：int [n]、char [n] ......

        n Number of elements , The number of elements is different , The type is different , Such as int [1] and int [2] Just different types

         Type of structure ：struct

         Enumeration type ：menu

         Joint type ：union

Pointer types ：

int* p、char* p、float* p、void* p ......

Empty type ：void

Usually used for function return types , Function parameter , Pointer types .

*C There is no string type in the language , Can only be stored by character array

Two 、 The storage of integers

         The original code, the reverse code, the complement code

Integers are stored in memory as complements .

Original code ： Convert integer to binary to get , The highest bit is the sign bit （1 It's a negative number ,0 Is a positive number ）

Inverse code ： The sign bit of the original code remains unchanged , Other bits are inversed to get

Complement code ： Inverse code +1 obtain

The original code of a positive number is the same as the complement of an inverse code .

Negative numbers need to be converted .

Why should integers be stored as complements in memory ？

This is because ：

1. Use complement , Symbol bits and value fields can be treated in a unified way , meanwhile , Addition and subtraction can also be handled in a unified way （ Convert subtraction to addition ）.

2. Complement and original code are converted to each other , The operation process is the same , No additional hardware circuits are required .

In a nutshell ：

Original code （ The sign bit remains the same and reverses by bit ）→ Inverse code （+1）→ Complement code

Complement code （ The sign bit remains the same and reverses by bit ）→ Inverse code （+1）→ Original code

  We can check the data stored in the variable to know whether the integer is stored as a complement in memory .

  It can be seen that integers store complements in memory , But the order is reversed , This is because of the problem of byte order at the size end .

         Byte order at the large and small end

Why is there big and small byte order ？

Low bytes are preferentially processed inside the computer , More efficient , So in most computers, small end storage mode is used , In other scenes , The big end storage mode is more efficient .

Big end ： Put the low order value in the high address , Put the high address into the low address .

The small end ： Put the low order value in the low address , Put the high address in the high address .

Under my compiler , The storage mode is small end .

         Exercise one

  Write a piece of code to judge the byte order of the size end of the current machine .

#include<stdio.h>
int main()
{
	int a = 1;
	if (*(char*)&a)// take a Cast address to char* type , You can only access backwards at a time 1 Bytes 
		printf(" The small end ");
	else
		printf(" Big end ");
	return 0;
}

         Exercise 2

Judge the output of the following code

 1.

int main()
{
	char a = -1;
	signed char b = -1;
	unsigned char c = -1;
	printf("a=%d,=%d,c=%d", a, b, c);
	return 0;
}

answer ：-1,-1,255

a and b They all print normally , Main analysis c

2. 

int main()
{
	char a = -128;
	printf("%u\n", a);
	return 0;
}

answer ：4294967168

 3.

int main()
{
	char a = 128;
	printf("%u\n", a);
	return 0;
}

answer ：4294967168

 4.

int main()
{
	int i = -20;
	unsigned int j = 10;
	printf("%d\n", i + j);
	return 0;
}

answer ：-10

5.

int main()
{
	unsigned int i;
	for (i = 9; i >= 0; i--)
	{
		printf("%u\n", i);
	}
	return 0;
}

answer ： Dead cycle .

int main()
{
	char a[1000];
	int i;
	for (i = 0; i < 1000; i++)
	{
		a[i] = -1 - i;
	}
	printf("%d", strlen(a));
	return 0;
}

answer ：255

First we need to know char The value range of the type is ：-128~127

Think of them as a circle .

Why? 10000000 yes -128

  meanwhile , We can also observe , In this ‘ egg ’ in , Just keep adding 1, You can get the next number , conversely , constantly -1, You can also get the next number .

Only when -1+1 when , You'll get 0, and strlen encounter 0 Will stop , because i It's from 0 At the beginning , So we just need to find out from 0 To 1 Just how many numbers there are between , At this time, we can see from the picture 0~1 It happens to be a whole cycle , There is a total of 255 A digital .

6.

unsigned char i = 0;
int main()
{
	for (i = 0; i <= 255; i++)
	{
		printf("hello world\n");
	}
	return 0;
}

answer ： Dead cycle

Unsigned char The value of type is 0~255, The duty of 255 Time again +1, It's back 1, Cycle again .

7.

int main()
{
	unsigned int a = -1;
	printf("%d", a);
	return 0;
}

answer ：-1

The printing result is subject to the printing type , Regardless of the original type of data .

-1 In memory for ：11111111111111111111111111111111

Although the type is unsigned int , But printing is based on int Type print , So we will judge this number as negative according to the sign bit , So it needs to be converted to the original code , Finally get -1.

8.

int main()
{
	if (strlen("abc") - strlen("abcdef") >= 0)
		printf(">");
	else
		printf("<");

	return 0;
}

answer ：>

because strlen The return type is size_t = unsigned int ( Unsigned integer ), And an unsigned integer minus an unsigned integer , The final result is unsigned integer , It can't be negative .

3、 ... and 、 Floating point storage

  Let's start with a piece of code , Look at its output .

int main()
{
	int n = 9;
	float* p = (float*)&n;

	printf("n The value of is ：%d\n", n);
	printf("*p The value of is ：%d\n", *p);

	*p = 9.0;
	printf("n The value of is ：%d\n", n);
	printf("p The value of is ：%d\n", *p);

	return 0;
}

Output results ：

Although I don't know why this is the result , But we can draw a preliminary conclusion ： Integer and floating-point numbers are stored in different ways in memory .

Floating point storage rules

  Any binary floating-point number can be expressed in the following form ：

V=(-1)^S*M*2^E

V Represents any floating-point number

S Represents the sign bit , When S=0 when ,V Is a positive number , When S=1 when ,V It's a negative number

M Represents a significant number , Greater than 1, Less than 2

E Indicates the index bit

And the last thing stored in memory is S、M、E These three values

Simply speaking , That is to write floating-point numbers in the form of scientific counting , Finally, add a plus or minus to the front .

  Inaccurate situation ：

Different types of floating-point number storage ：

  about 32 Floating point number of bits (float), The highest bit is the sign bit S, next 8 Bits are exponents E, be left over 23 Bits are valid letters M

  about 64 Floating point number of bits (double), The highest bit is the sign bit S, next 11 Bits are exponents E, be left over 52 Bits are valid letters M

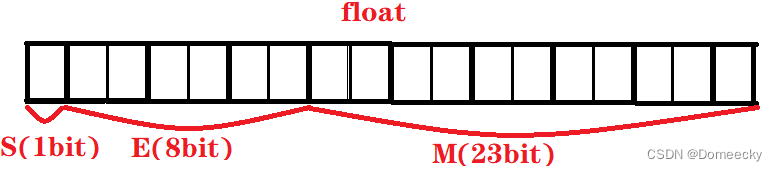
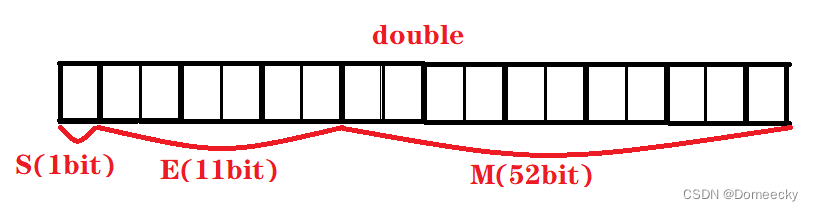
  When storing floating point numbers , There are also the following rules ：

1. because M Always with 1 start , So will M When it's in memory , Omit the beginning 1, When taking out the data, add . In this way, you can save one more digit , Improve data accuracy .

2. take E The value of is set to unsigned , This can store more data .

On the second point, there is a problem , Because of our E It is possible to have negative numbers .

At this time , In order not to have negative numbers , It is stipulated in E In memory , You need to add a middle number ,float The median number under type is 127,double The median number under type is 1023

for example , stay float Next E by 2 when , The value stored in memory is 2+127=129, It's written as binary 10000001

Verify storage rules ：

  When taking out floating-point numbers , There are three situations ：

1. E Incomplete 0 Or not all 1

Subtract the value of the index 127（ or 1023）, Get the real value , And then the significant number M Add the omitted 1, Get the original value , Perform normal operation .

2. E For all 0

Direct will E The value is equal to the 1-127= - 126,M It doesn't add 1, But to become 0, In order to express 0 Or close to 0 The number of .

3. E For all 1

Expressed as positive and negative infinity

Explain the topic ：

int main()
{
	int n = 9;
	float* p = (float*)&n;

	printf("n The value of is ：%d\n", n);
	printf("*p The value of is ：%d\n", *p);

	*p = 9.0;
	printf("n The value of is ：%d\n", n);
	printf("p The value of is ：%d\n", *p);

	return 0;
}