当前位置:网站首页>Understanding the mathematical essence of machine learning
Understanding the mathematical essence of machine learning
2022-07-26 05:58:00 【Datawhale】
Datawhale dried food
author : Academician ewenan , source : Scientific intelligence AISIBeijing time. 2022 year 7 month 8 On Tuesday night 22:30, Academician ewenan stay 2022 Year of International Congress of mathematicians Last work One hour Conference Report (plenary talk). Today we'll share the content of teacher e's speech . Mr. e first shared his understanding of Understanding the mathematical essence of machine learning ( Function approximation 、 Approximation and sampling of probability distribution 、Bellman The solution of the equation ); Then it introduces the machine learning model Approximation error 、 Mathematical theory of generalization and training ; Finally, it introduces how to use machine learning to Solve difficult scientific calculations and scientific problems , namely AI for science. The authors Hertz.

The mathematical nature of machine learning problems
as everyone knows , The development of machine learning , It has completely changed people's understanding of artificial intelligence . Machine learning has many amazing achievements , for example :
· Recognize pictures more accurately than humans : Use a set of marked pictures , Machine learning algorithm can accurately identify the category of pictures :

Cifar-10 problem : Divide the pictures into ten categories
source :https://www.cs.toronto.edu/~kriz/cifar.html
· Alphago Next go Defeat humanity : The algorithm of playing go is completely realized by machine learning :
Reference resources :https://www.bbc.com/news/technology-35761246
· Generate face pictures , achieve The setup The effect of :

Reference resources :https://arxiv.org/pdf/1710.10196v3.pdf
Machine learning has many other applications . In everyday life , People even often use the services provided by machine learning without knowing , for example : Spam filtering in our email system 、 Speech recognition in our cars and mobile phones 、 The fingerprint in our mobile phone is unlocked ……
All these great achievements , Essentially , But success Solved some classical mathematical problems .
*
For image classification , What we are interested in is actually functions ![]() :
:
![]() : Images → Category
: Images → Category
function ![]() Map the image to the category that the image belongs to . We know
Map the image to the category that the image belongs to . We know ![]() The value on the training set , I want to find the right function
The value on the training set , I want to find the right function ![]() A good enough Close to .
A good enough Close to .
generally speaking , Supervised learning (supervised learning) problem , The essence is to be based on a limited training set S, Give an efficient of the objective function Close to .
*
For face generation , Its essence is Approximate and sample an unknown probability distribution . In this case ,“ Face ” It's a random variable , And we don't know its probability distribution . However , We have “ Face ” The sample of : A huge number of face photos . We can use these samples , Approximate result “ Face ” Probability distribution of , And thus generate new samples ( That is, generate a face ).
generally speaking , The essence of unsupervised learning is Using limited samples , Approximate and sample the unknown probability distribution behind the problem .
*
For those who play go Alphago Come on , If the opponent's strategy is given , The dynamics of go is the solution of a dynamic programming problem . Its optimal strategy satisfies Bellman equation . thus Alphago The essence of is to solve Bellman equation .
generally speaking , Reinforcement learning In essence, it is to solve The optimal strategy of Markov process .
However , These questions are Computational Mathematics Classic problems in the field !! After all , Function approximation 、 Approximation and sampling of probability distribution , And the numerical solution of differential equations and difference equations , Are extremely classic problems in the field of Computational Mathematics . that , These problems are in the context of machine learning , What is the difference between it and classical computational mathematics ? The answer is :
dimension (dimensionality)
for example , In the problem of image recognition , The dimensions entered are ![]() . For classical numerical approximation methods , about
. For classical numerical approximation methods , about ![]() Dimensional problem , contain
Dimensional problem , contain ![]() Approximation error of a model with parameters
Approximation error of a model with parameters ![]() . In other words , If you want to reduce the error 10 times , The number of parameters needs to be increased
. In other words , If you want to reduce the error 10 times , The number of parameters needs to be increased ![]() . When dimension
. When dimension ![]() increases , The calculation cost increases exponentially . This phenomenon is often called :
increases , The calculation cost increases exponentially . This phenomenon is often called :
Dimension disaster (curse of dimensionality)
All classic algorithms , For example, polynomial approximation 、 Wavelet approximation , Are suffering from dimensional disasters . Obviously , The success of machine learning tells us , In high dimensional problems , Deep neural network The performance of is much better than the classical algorithm . However , such “ success ” How to do it ? Why in high-dimensional problems , No other way , but Deep neural network It has achieved unprecedented success ?
Starting from Mathematics , Understand machine learning “ Black magic ”: Mathematical theory of supervised learning
2.1 Marking and setting
Neural network is a special kind of function . such as , The two-layer neural network is :

There are two sets of parameters ,![]() and
and ![]() .
.![]() Is the activation function , It can be :
Is the activation function , It can be :
· ![]() ,ReLU function ;
,ReLU function ;
· ![]() ,Sigmoid function .
,Sigmoid function .
The basic component of neural network is : Linear transformation and one-dimensional nonlinear transformation . Deep neural network , Generally, it is the composition of the following structures :
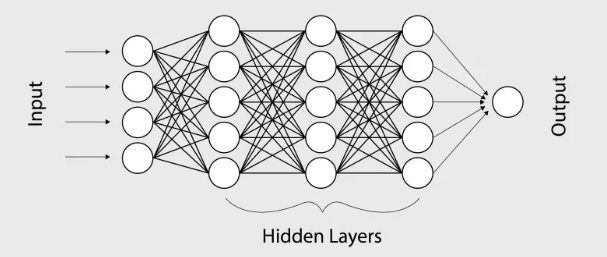

For simplicity , We omit all here bias term ![]() .
.![]() It's the weight matrix , Activation function
It's the weight matrix , Activation function ![]() Act on every component .
Act on every component .
We will be in the training set S Upper approximation of the objective function ![]()

Hypothetical hypothesis ![]() The domain of definition of is
The domain of definition of is ![]() . Make
. Make ![]() by
by ![]() The distribution of . Then our goal is : Minimize test errors
The distribution of . Then our goal is : Minimize test errors ![]() (testing error, Also known as population risk or generalization error):
(testing error, Also known as population risk or generalization error):

2.2 Error of supervised learning
Supervised learning generally has the following steps :
*
First step : Choose a hypothetical space ( A set of test functions )![]() (m Directly proportional to the dimension of the test space );
(m Directly proportional to the dimension of the test space );
*
The second step : Choose a loss function to optimize . Usually , We will choose empirical error (empirical risk) To fit the data :

Sometimes , We will add other penalties .
*
The third step : Solving optimization problems , Such as :
· gradient descent :

· Stochastic gradient descent :

![]() It's from 1,…n A random selection of .
It's from 1,…n A random selection of .
If you record the output of machine learning ![]() , Then the total error is
, Then the total error is ![]() . Let's redefine :
. Let's redefine :
*
![]() Is the best approximation in the hypothetical space ;
Is the best approximation in the hypothetical space ;
*
![]() In hypothetical space , Based on data sets S The best approximation .
In hypothetical space , Based on data sets S The best approximation .
thus , Then we can divide the error into three parts :

*
![]() Is the approximation error (approximation error): It is completely determined by the selection of hypothetical space ;
Is the approximation error (approximation error): It is completely determined by the selection of hypothetical space ;
*
![]() Is the estimation error (estimation error): Additional error due to limited data set size ;
Is the estimation error (estimation error): Additional error due to limited data set size ;
*
![]() Is the optimization error (optimization error): By training ( Optimize ) Additional errors .
Is the optimization error (optimization error): By training ( Optimize ) Additional errors .
2.3 Approximation error
Let's focus on approximation error (approximation error).
Let's make a comparison with the traditional Fourier transform :
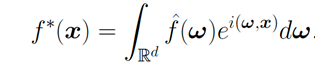
If we use discrete Fourier transform to approximate :

Its error ![]() Is proportional to
Is proportional to ![]() , Undoubtedly affected by dimensional disasters .
, Undoubtedly affected by dimensional disasters .
And if a function can be expressed in the desired form :

Make ![]() It's a measure
It's a measure ![]() Independent identically distributed samples , We have :
Independent identically distributed samples , We have :

Then the error at this time is :

You can see , This is independent of dimension !
If the activation function is ![]() , that
, that ![]() That is to say
That is to say ![]() A two-layer neural network for activation function . This result means : This kind of ( It can be expressed as expectation ) Function of , Can be approached by two-layer neural network , And forced The rate of near error is independent of dimension !
A two-layer neural network for activation function . This result means : This kind of ( It can be expressed as expectation ) Function of , Can be approached by two-layer neural network , And forced The rate of near error is independent of dimension !
For general double-layer Neural Networks , We can get a series of similar approximation results . The key problem is : What kind of function can be approximated by double-layer neural network ? So , We introduce Barron The definition of space :

Barron The definition of space
Reference resources :E, Chao Ma, Lei Wu (2019)
For arbitrary Barron function , There is a two-layer neural network ![]() , Its approximation error satisfies :
, Its approximation error satisfies :

It can be seen that this approximation error is independent of dimension !( Details about this part of the theory , You can refer to :E, Ma and Wu (2018, 2019), E and Wojtowytsch (2020). Other things about Barron space Classification theory , You can refer to Kurkova (2001), Bach (2017),
Siegel and Xu (2021))
Similar theories can be extended to residual neural networks (residual neural network). In residual neural network , We can use stream - Induced function space (flow-induced function space) replace Barron Space .
2.4 Generalization : The difference between training error and testing error
People usually expect , The difference between training error and testing error will be proportional to ![]() (n Is the number of samples ). However , Our trained machine learning model is strongly correlated with the training data , This leads to this Monte-Carlo Rate does not necessarily hold . So , We give the following generalization theory :
(n Is the number of samples ). However , Our trained machine learning model is strongly correlated with the training data , This leads to this Monte-Carlo Rate does not necessarily hold . So , We give the following generalization theory :

in short , We use it Rademacher Complexity is used to describe the ability of a space to fit random noise on the data set .Rademacher Complexity is defined as :

among ![]() The value is 1 or -1 Independent identically distributed random variables of .
The value is 1 or -1 Independent identically distributed random variables of .
When ![]() It's the unit ball time in lippossis space , Its Rademacher Complexity is proportional to
It's the unit ball time in lippossis space , Its Rademacher Complexity is proportional to ![]() .
.
When d increases , It can be seen that the sample size index required for fitting increases . This is actually another form of dimensional disaster .
2.5 Mathematical understanding of the training process
On the training of neural networks , There are two basic problems :
*
Whether the gradient descent method can converge quickly ?
*
The result of training , Is there a better generalization ?
For the first question , I'm afraid the answer is pessimistic .Shamir(2018) The lemma in tells us , Gradient based training method , Its convergence rate is also affected by dimensional disasters . As mentioned above Barron space, Although it is a good means to establish approximation theory , But there is too much space for training to understand neural networks .
Specially , Such a negative result can be highly hyperparametric (highly over-parameterized regime) The circumstances of ( namely m>>n) Get a specific description . In this case , The dynamics of parameters appears Scale separation The phenomenon of : For the following two-layer neural network :

In the process of training ,![]() The dynamics of are :
The dynamics of are :

From this, we can see the phenomenon of scale separation : When m Very big time ,![]() The dynamics of is almost frozen .
The dynamics of is almost frozen .
In this case , The good news is that we have exponential convergence (Du et al, 2018); The bad news is this time , Neural networks are no better than those from random feature model Good model .
We can also understand the gradient descent method from the perspective of mean field . Make :![]() , And order :
, And order :

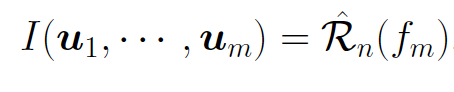
be ![]() Is the solution of the following gradient descent problem :
Is the solution of the following gradient descent problem :

If and only if ![]() Is the solution of the following equation ( Reference resources :Chizat and Bach (2018), Mei, Montanari and Nguyen (2018), Rotsko and Vanden-Eijnden (2018), Sirignano and Spiliopoulos (2018)):
Is the solution of the following equation ( Reference resources :Chizat and Bach (2018), Mei, Montanari and Nguyen (2018), Rotsko and Vanden-Eijnden (2018), Sirignano and Spiliopoulos (2018)):

This mean field dynamics , It's actually in the Wassenstein Gradient dynamics in the sense of metrics . People have proved : If its initial value ![]() The support of is the whole space , And the gradient descent does converge , Then the convergence result must be global optimization ( Reference resources :Chizat and Bach (2018,2020), Wojtowytsch (2020)).
The support of is the whole space , And the gradient descent does converge , Then the convergence result must be global optimization ( Reference resources :Chizat and Bach (2018,2020), Wojtowytsch (2020)).
Application of machine learning
3.1 Solve the problem of high-dimensional Scientific Computing
Since machine learning is an effective tool for dealing with high-dimensional problems , We can use machine learning to solve problems that are difficult to deal with by traditional computational mathematics .
The first example is Stochastic control problem . Traditional methods to solve stochastic control problems need to solve an extremely high-dimensional Bellman equation . Using machine learning methods , It can effectively solve stochastic control problems . Its idea is quite similar to the residual neural network ( Reference resources Jiequn Han and E (2016)):
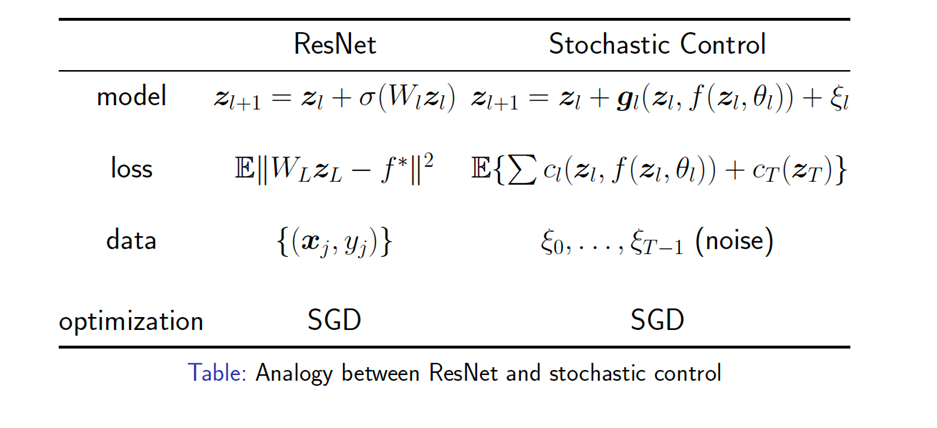
The second example is Solve nonlinear parabolic equation . The nonlinear parabolic equation can be rewritten as a stochastic control problem , Its minimum point is unique , Corresponding to the solution of nonlinear parabolic equation .

3.2 AI for science
The ability to use machine learning to deal with high-dimensional problems , We can solve more scientific problems . Here we give two examples . The first example is Alphafold.

Reference resources :J. Jumper et al. (2021)
Second example , It's our own work : Deep potential molecular dynamics (DeePMD). This is what can be achieved Ab initio precision molecular dynamics . The new simulation we used “ normal form ” That is :
*
Using the first principles of quantum mechanics to calculate and provide data ;
*
Using neural networks , Give an accurate... Of the potential energy surface fitting ( Reference resources :Behler and Parrinello (2007), Jiequn Han et al (2017), Linfeng Zhang et al (2018)).
Application DeePMD, We can simulate a series of materials and molecules , You can achieve The calculation accuracy of the first level :

We have also achieved Simulation of the first principle accuracy of 100 million atoms , To obtain the 2020 Gordonbell award in :

Reference resources :Weile Jia, et al, SC20, 2020 ACM Gordon Bell Prize
We have given Phase diagram of water :
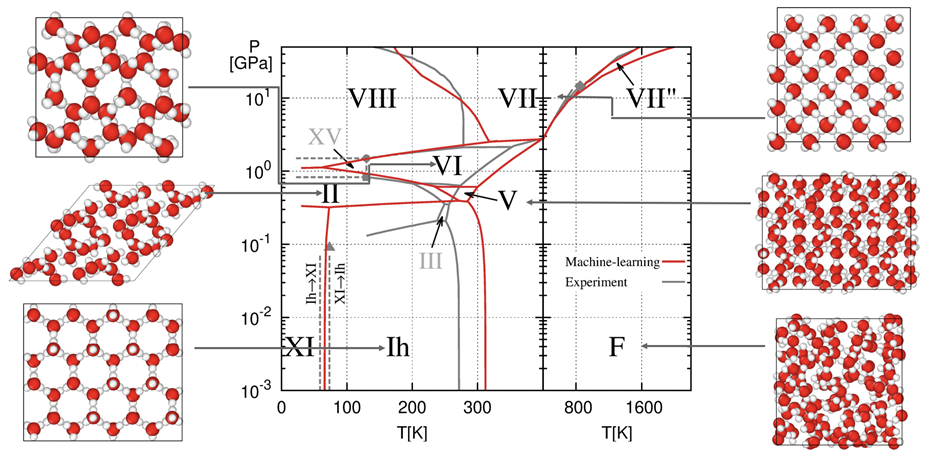
Reference resources :Linfeng Zhang, Han Wang, et al. (2021)
As a matter of fact , Physical modeling spans multiple scales : Macroscopic 、 mesoscopic 、 Microcosmic , and Machine learning happens to provide tools for cross scale modeling .

AI for science, That is to use machine learning to solve scientific problems , There have been a series of important breakthroughs , Such as :
*
Quantum many body problem :RBM (2017), DeePWF (2018), FermiNet (2019),PauliNet (2019),…;
*
Density functional theory : DeePKS (2020), NeuralXC (2020), DM21 (2021), …;
*
Molecular dynamics : DeePMD (2018), DeePCG (2019), …;
*
Kinetic equations : Machine learning moment closure (Han et al. 2019);
*
Continuum dynamics : ![]() (2020)
(2020)
In the next five to ten years , It is possible for us to : Modeling and computing across all physical scales . This will completely change how we solve practical problems : Such as drug design 、 material 、 Combustion engine 、 catalysis ……

summary
Machine learning is basically a mathematical problem in high dimension . Neural network is an effective means of high-dimensional function approximation ; This is the field of artificial intelligence 、 The field of science and technology offers many new possibilities .
This has also created a new theme in the field of Mathematics : High dimensional analysis . In short , It can be summarized as follows :
*
Supervised learning : High dimensional function theory ;
*
Unsupervised learning : High dimensional probability distribution theory ;
*
Reinforcement learning : High dimensional Bellman equation ;
*
Time series learning : High dimensional dynamical system .

About AISI
Beijing Institute of scientific intelligence (AI for Science Institute, hereinafter referred to as AISI) Founded on 2021 year 9 month , Led by academician ewenan , We are committed to combining AI technology with scientific research , Accelerate the development and breakthroughs in different scientific fields , Promote the innovation of scientific research paradigm , Build a world leading 「AI for Science」 Infrastructure system .
AISI Of the researchers come from top universities at home and abroad 、 Scientific research institutions and scientific and technological enterprises , Common focus on physical modeling 、 Numerical algorithms 、 Artificial intelligence 、 Core issues in cross cutting areas such as high-performance computing .
AISI Committed to creating an academic environment where ideas collide , Encourage free exploration and cross-border cooperation , Jointly explore new possibilities for the combination of artificial intelligence and scientific research .

Sorting is not easy to , spot Fabulous Three even ↓
边栏推荐
- Is it really hopeless to choose electronic engineering and be discouraged?
- Mysql45 talks about transaction isolation: why can't I see it after you change it?
- Learn about spark project on nebulagraph
- Byte interview question - judge whether a tree is a balanced binary tree
- Sequential search, half search, block search~
- 金仓数据库 KingbaseES SQL 语言参考手册 (6. 表达式)
- Embedded general learning route arrangement
- leetcode-aboutString
- leetcode-Array
- Kingbasees SQL language reference manual of Jincang database (6. Expression)
猜你喜欢

Why can't lpddr completely replace DDR?

Kingbasees SQL language reference manual of Jincang database (8. Functions (XI))

软件测试面试题全网独家没有之一的资深测试工程师面试题集锦

Another open source artifact, worth collecting and learning!
Redis persistence AOF

Kingbasees SQL language reference manual of Jincang database (6. Expression)

Redis主从复制
![ERROR: Could not open requirements file: [Errno 2] No such file or directory: ‘requirments.txt’](/img/15/25ff1e544565e18319ecca85e614a2.png)
ERROR: Could not open requirements file: [Errno 2] No such file or directory: ‘requirments.txt’

CANoe-XML在Test Modules中的应用

Qu Weihai, chairman and CEO of Xinyi interactive, adheres to mutual benefit and win-win results, and Qu Weihai promotes enterprise development
随机推荐
Binary sort tree (BST)~
Use latex to typeset multiple-choice test paper
MBA-day29 算术-绝对值初步认识
【Oracle SQL】计算同比与环比(列转行进行偏移)
Redis持久化-RDB
leetcode-Array
Ros2 knowledge: DDS basic knowledge
Kingbasees SQL language reference manual of Jincang database (11. SQL statement: abort to alter index)
Lemon class automatic learning after all
语法泛化三种可行方案介绍
Redis persistence AOF
NFT in the eyes of blackash: the platform is crying for slaughter, and users send money to the door
Kingbasees SQL language reference manual of Jincang database (7. Conditional expression)
Interview questions for software testing is a collection of interview questions for senior test engineers, which is exclusive to the whole network
Kingbasees SQL language reference manual of Jincang database (9. Common DDL clauses)
Who is responsible for the problems of virtual idol endorsement products? And listen to the lawyer's analysis
leetcode-Array
ERROR: Could not open requirements file: [Errno 2] No such file or directory: ‘requirments.txt’
[highly available MySQL solution] centos7 configures MySQL master-slave replication
二叉树的性质 ~